Today I had an excellent idea, only to discover that someone had already had that excellent idea some time ago.

I’m in the process of designing and writing an npm module, but before I go ahead and write it I want some feedback on whether it’s going to be useful. Rather writing a docs/slides/e-mails to descibe what I intend doing I had my excellent (but, it turns out, unoriginal) idea…

“Why don’t I write the README.md that I’d expect to check into GitHub, get some feedback, and then write either write the code or adjust the README.md until the feedback is good!? Hey! I’ve just invested README Driven Development!!”

It turns out it’s not a stupid idea, and because of this Tom Preston-Werner blogged about it in 2010….

http://tom.preston-werner.com/2010/08/23/readme-driven-development.html

Anyway….it’s a good idea, even if it’s not an original idea, and I’m finding it very useful.

I make sure my README.md has the following parts:

1. Installation (how will people get the code once I’ve written it)
2. Code examples of it in action (the cannonical use cases for what you’re wrting)
3. Links to further reading (information that will be useful to the user of your code)

I want to make sure that others can quickly give feedback that the approach makes sense, the sample code looks good, and that they’d want to use the code. If you can’t write a README for what you’re about to build, show it to people, and have them say “Hey! That would be really useful!” then you need to ask yourself to hard questions about what you’re writing and whether it has value.

If you take this to an extreme, perhaps you should only start writing the code when your GitHub repo gets some stars, or people start opening issues saying “Where’s the code? I want to install this package and can’t find it on npm!”. Thsi would be similar to Lean Startup techniques where interest in a service or product is determined by building a basic marketing site and seeing if people click the “buy now” button, or sign up for more information.

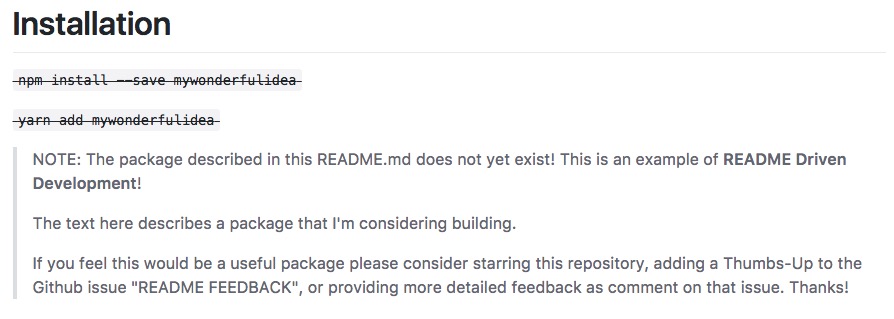
One thing to keep in mind if you’re doing this in public on Github: make it clear, somewhere near the top of your README.md, that the library/code/package you’re describing doesn’t exist yet. I like to include this in the Installation section of the README.md, by striking out the actual instructions and adding a note like this…